www.brix.de - Hauptseite, Elektrotechnik
|
Stand: 2024-12-15
|
|
Im Folgenden geht es um den Strom im Neutralleiter im haushaltsüblichen Drehstromnetz. Es werden Fälle symmetrischer und unsymmetrischen Belastung betrachtet. Außerdem wird auf die Auswirkung auf den Strom im Neutralleiter im Fall der Phasenverschiebung zwischen den Außenleitern (L1, L2, L3) eingegangen. Am Ende der Diskussion wird die "Kompensation" als eine wirksame Gegenmaßnahme grundsätzlich beschrieben. Nicht betrachtet werden die Auswirkungen von Oberwellen auf den Strom im Neutralleiter.
Diese Darstellung verwendet qualitative Zeigerdiagramme. Das ist eine relativ einfache Darstellung der im Detail komplizierteren "Vektorrechnung". Vor Zeigerdiagrammen darf man, wenn es um Drehstrom geht, keine Scheu haben. Sie verdeutlichen ohne aufwändige trigonometrische Formeln die Zusammenhänge der in den Außenleitern fließenden Ströme.
Hinweis: Selbstverständlich kann man mit Zeigerdiagrammen auch wirklich grafisch "rechnen", wenn man die Pfeile ("Zeiger") maßstäblich einzeichnet und die Länge und den Phasenwinkel des sich ergebenden Pfeiles mit dem Geodreieck misst. Bei einigermaßen sorgfältiger Arbeit, ergeben sich erstaunlich genaue Ergebnisse!
Es geht hier ausschließlich um Sternschaltungen. Nur diese haben überhaupt einen Neutralleiter. Dreieckschaltung haben grundsätzlich keinen, so dass die Frage nach den Strömen in einer Dreieckschaltunng auf die Außenleiter beschränkt bleibt.
Auch der Ausfall (Bruch oder Abriss) des Neutralleiters und die daraus resultierenden Spannungen über die Stränge (die sogenannte "Sternpunktverschiebung") ist nicht Gegenstand dieser Darstellung.
Der Strom durch die drei Stränge des Drehstromsystems wird durch die konstante Spannung zwischen Außen- und Neutralleiter eingeprägt. Er hängt vom Widerstand oder genauer von der Impedanz eines einzelnen Stranges ab. Da es einen Neutralleiter im Sternpunkt gibt, sind die Ströme der drei Stränge voneinander unabhängig, die Spannung eines jeden Stranges ist, wie eingangs gesagt, konstant.
Ebenfalls konstant ist die Phasenlage der drei Spannungen. Sie sind zueinander um jeweils 120° verschoben. Die Phasenlage eines jeden Strangstromes hängt dagegen von dessen Impedanz ab. Bei induktiven Widerständen eilt der Strom der Spannung nach, bei kapazitiven Widerständen entsprechend voraus.
In der Darstellung hier sind L1, L2 und L3 im Uhrzeigersinn angeordnet, was "mathematisch negativ" drehend ist. Oft finden sich auch Darstellungen mit L1, L2 und L3 in mathematisch positiver Reihenfolge gegen den Uhrzeigersinn. Das spielt aber für die Betrachtung hier keine Rolle.
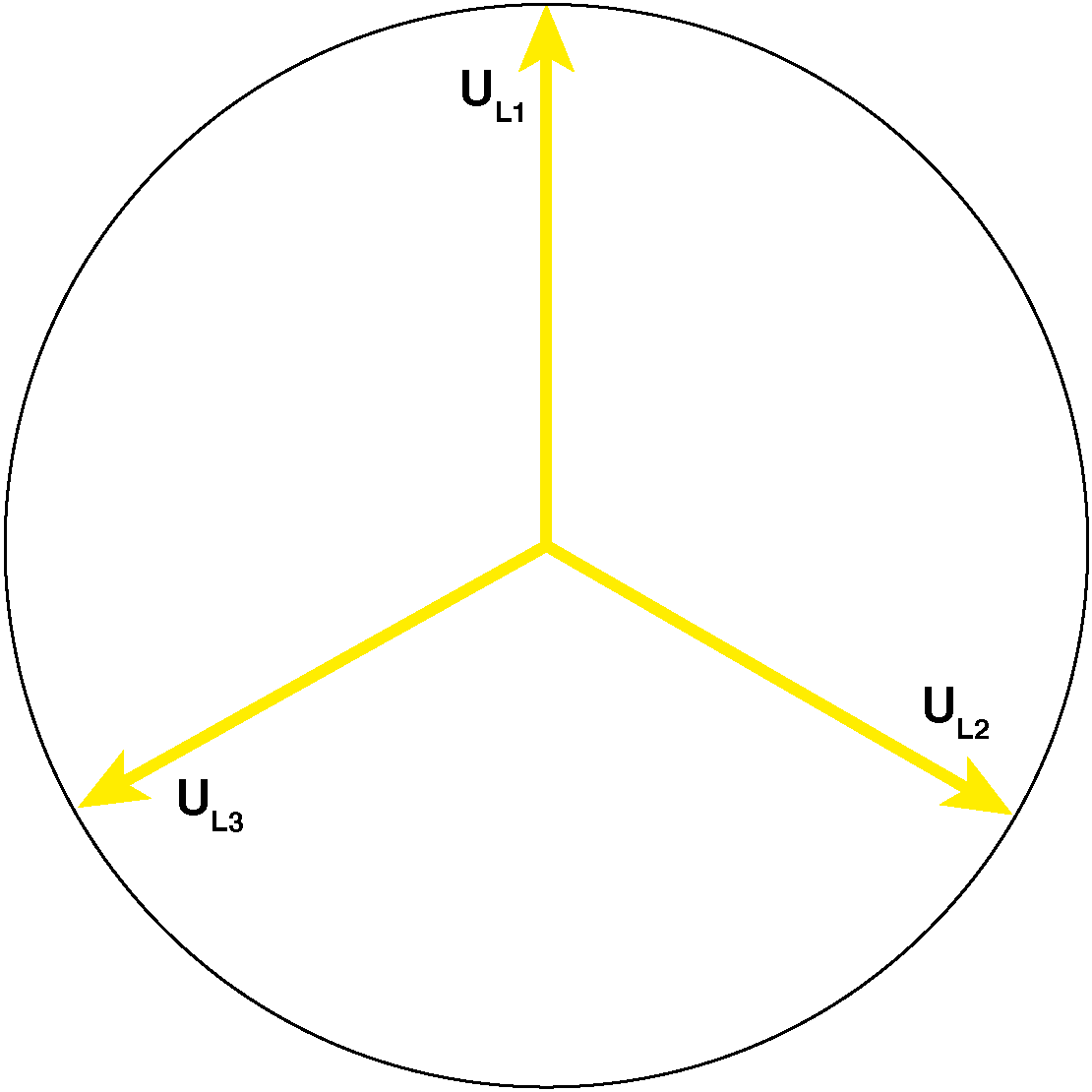
In allen im Folgenden dargestellten Fällen sind die Spannungen 120° phasenverschoben und in Größe und Phasenlage konstant. Wenn sich also Ströme ändern, liegt das daran, dass sich der Widerstand (die Impedanz) im jeweiligen Strang verändert an. Praktisch heißt dies nichts anderes, als dass ein weiterer Verbraucher zugeschaltet oder ein vorhandener Verbraucher abgeschaltet wird. Die Verbraucher eines Stranges liegen alle parallel zwischen Außen- und Neutralleiter.
Nebenstehend symbolisieren die Pfeile die Größe und die Phasenlage der Strangspannungen. Die Darstellung ist rein qualitativ, der Maßstab ist willkürlich gewählt und hier unwichtig.
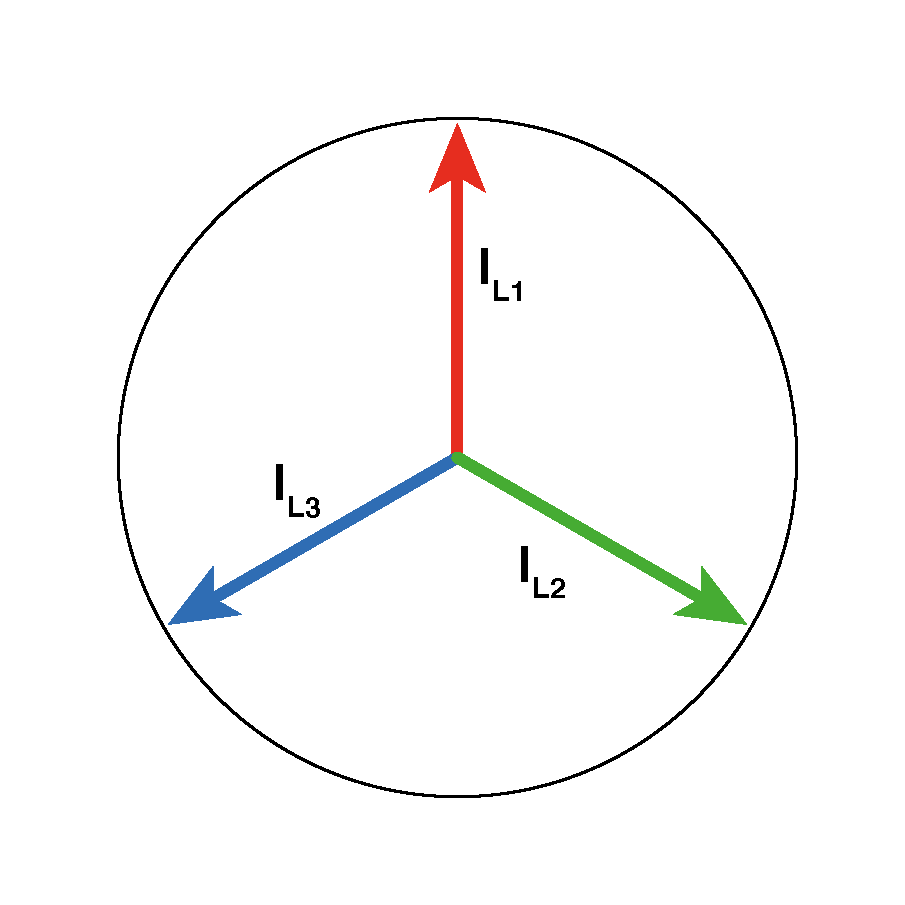
In allen im Folgenden dargestellten Zeigerdiagrammen symbolisieren die Pfeile die Größe und die Phasenlage der Strangströme. Je länger der Pfeil, desto größer der Strom. Der Winkel auf dem Kreis zeigt die Phasenlage desselben. Die eingezeichneten Kreise dienen dazu, die Längen der Zeiger zueinander besser abschätzen zu können. Sie haben ansonsten keine Bedeutung für das Zeigerdiagramm.


Die drei Strangströme sind gleich groß und in Phase zur jeweiligen Spannung. Wenn man alle drei Ströme grafisch addiert, ist der Abstand zwischen der Spitze des letzten Strompfeiles und dem Sternpunkt die Größe des Stromes, der im Neutralleiter fließt.
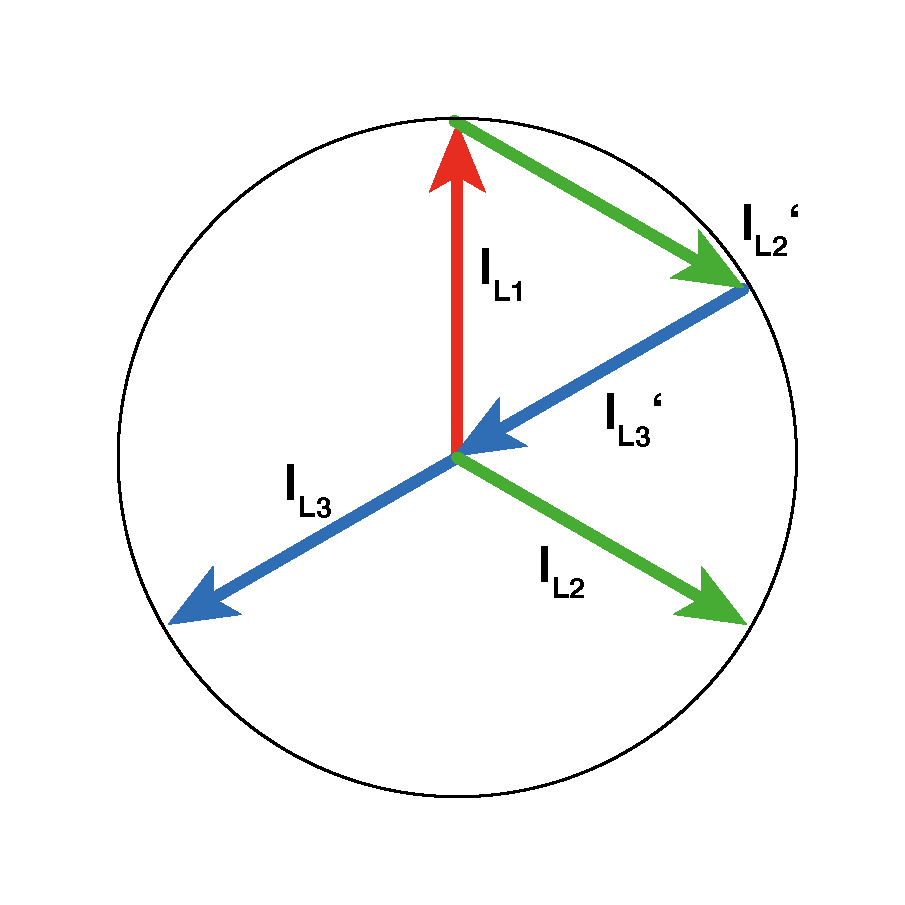
"Grafisch addieren" bedeutet, dass man die Pfeile, ohne sie zu verdrehen oder zu verlängern oder zu verkürzen, jeweils mit Pfeilende an Pfeilspitze legt. Die Pfeile IL2' und IL3' sind also nur die parallel verschobenen Pfeile IL2 und IL3.
Welche Pfeile man verschiebt und in welcher Reihenfolge sie aneinander gelegt werden, spielt für das Ergebnis keine Rolle. Mathematisch heißt das "Vektoradditionen sind kommutativ" (es gilt das "Vertauschungsgesetz").
Da die Pfeilspitze von IL3' im Sternpunkt endet, folgt daraus, dass der Strom im Neutralleiter "Null" ist. - Man könnte den Neutralleiter "weglassen" oder "abklemmen" und die Verhältnisse würden sich nicht ändern.
IN = 0
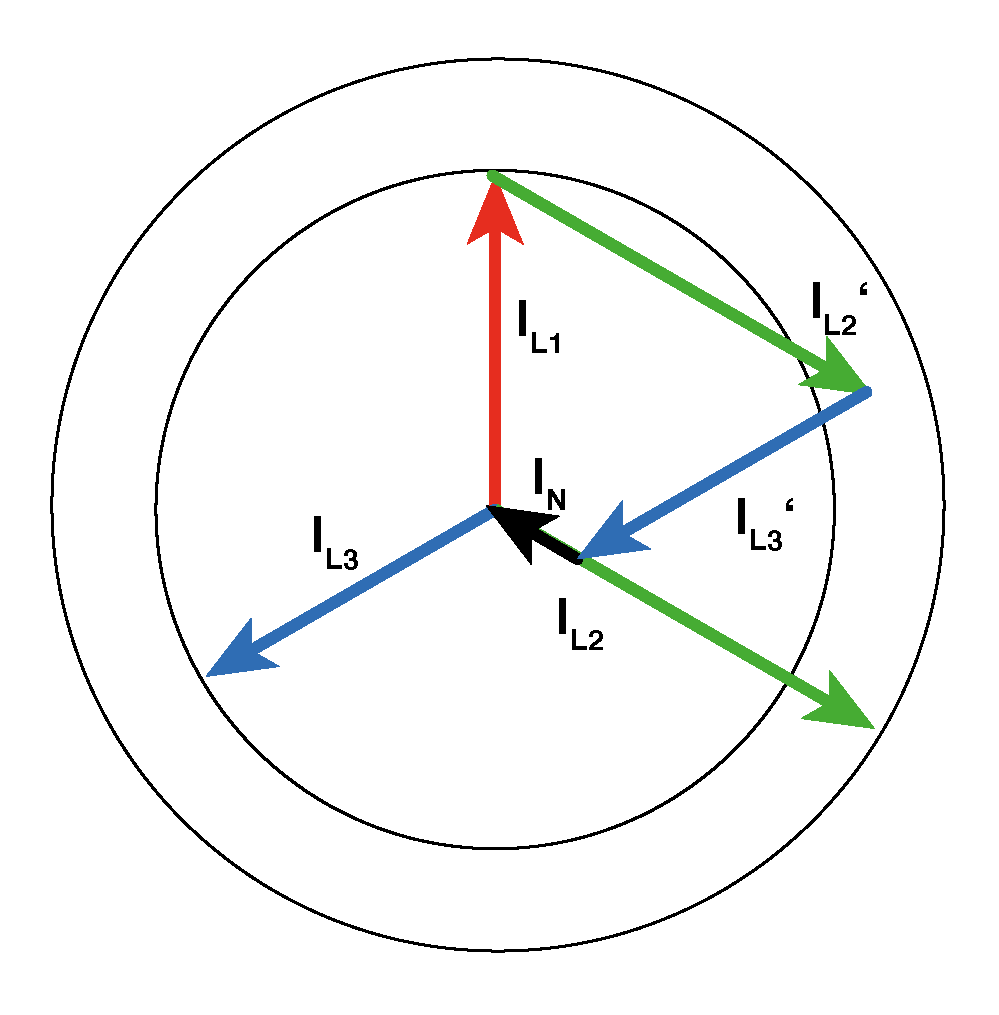
Der Strom IL2 ist größer als die gleich großen Ströme IL1 und IL3.
Die grafische Addition der drei Ströme ergibt nun, dass die Pfeilspitze von IL3' nicht mehr im Sternpunkt, sondern "auf IL2" endet. - Und zwar genau soweit von Sternpunkt entfernt, wie IL2 größer ("länger") als IL1 und IL3 ist.
Nun fließt also ein (relativ kleiner) Strom IN, der in Phase zum Strom IL2 liegt.
Würde der Neutralleiter "brechen" oder "abreißen" würden sich die Verhältnisse der Spannungen und Ströme durch eine sogenannte Sternpunktverschiebung ändern. Dieser Fall wird hier aber nicht weiter betrachtet.
Im speziellen hier gezeichneten Fall ist der Strom IN kleiner als IL2 und sogar kleiner als IL1 bzw. IL3. Letzteres ist aber keine allgemeine Regel. Wenn man sich vorstellt, IL2 noch wesentlich zu vergrößern, dann landet die Pfeilspitze von IL3' irgendwann außerhalb des Kreises von IL1 und IL3. Das heißt im Allgemeinen gilt in diesem Fall nur IN ist auf jeden Fall kleiner als IL2.
Allgemein:
IL2 > IN > 0
Phasenlage von IN ist gleich der Phasenlage von IL2
hier im speziellen Fall:
IL2 > IL1 > IN > 0
außerdem gilt IL1 = IL2
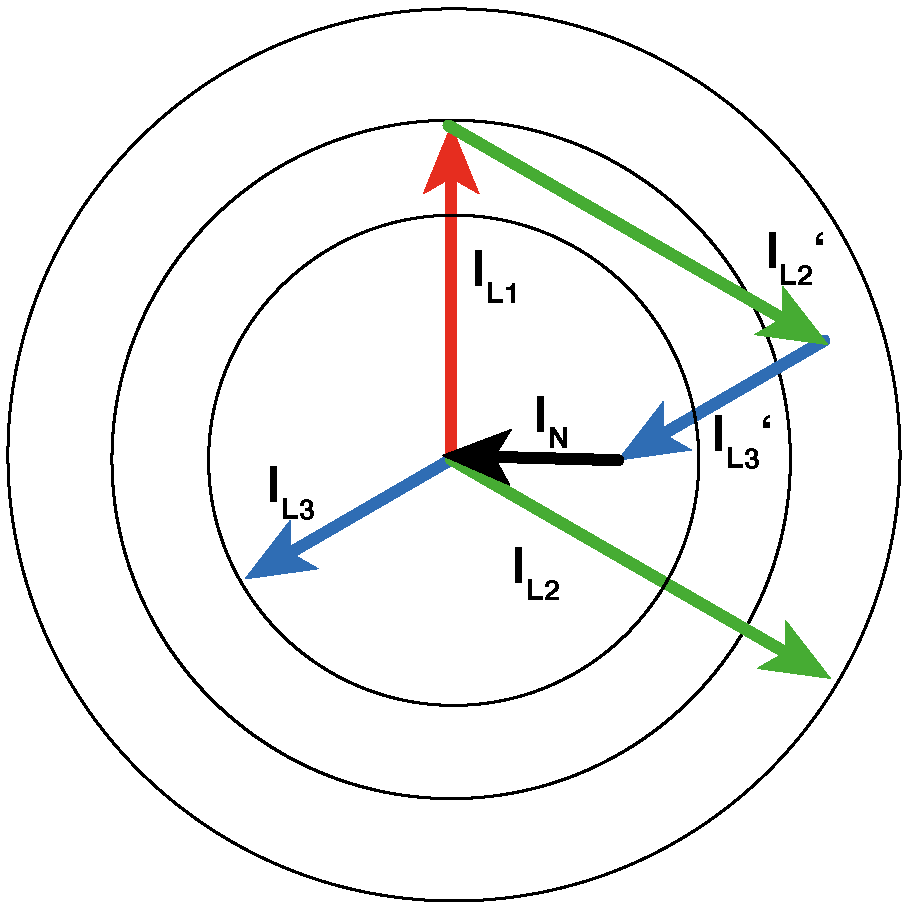
In allen drei Außenleitern fließen unterschiedlich große Ströme: IL1 =/= IL2 =/= IL3.
In diesem allgemeinen Fall endet die Pfeilspitze von IL3' nach der grafische Addition nicht mehr auf dem Zeiger eines anderen Stromes und sowieso nicht im Sternpunkt, sondern in einem nicht besonders ausgezeichneten Punkt des Zeigerdiagrammes, je nach Größe der einzelnen Strangströme.
Wieder ist der Abstand der Pfeilspitze von IL3' zum Sternpunkt die Größe und Phasenlage des IN. IN ist auf jeden Fall kleiner als IL2 und sein Phasenwinkel liegt zwischen IL1 und IL2. Je größer IL2, desto größer IN und um so mehr nähert sich die Phasenlage von IN der von IL2 an.
Allgemein:
IL2 > IN > 0
oder:
IN ist kleiner als der größte Strangstrom.
Die Phasenlage von IN ist ungleich der Phasenlage aller Strangströme.
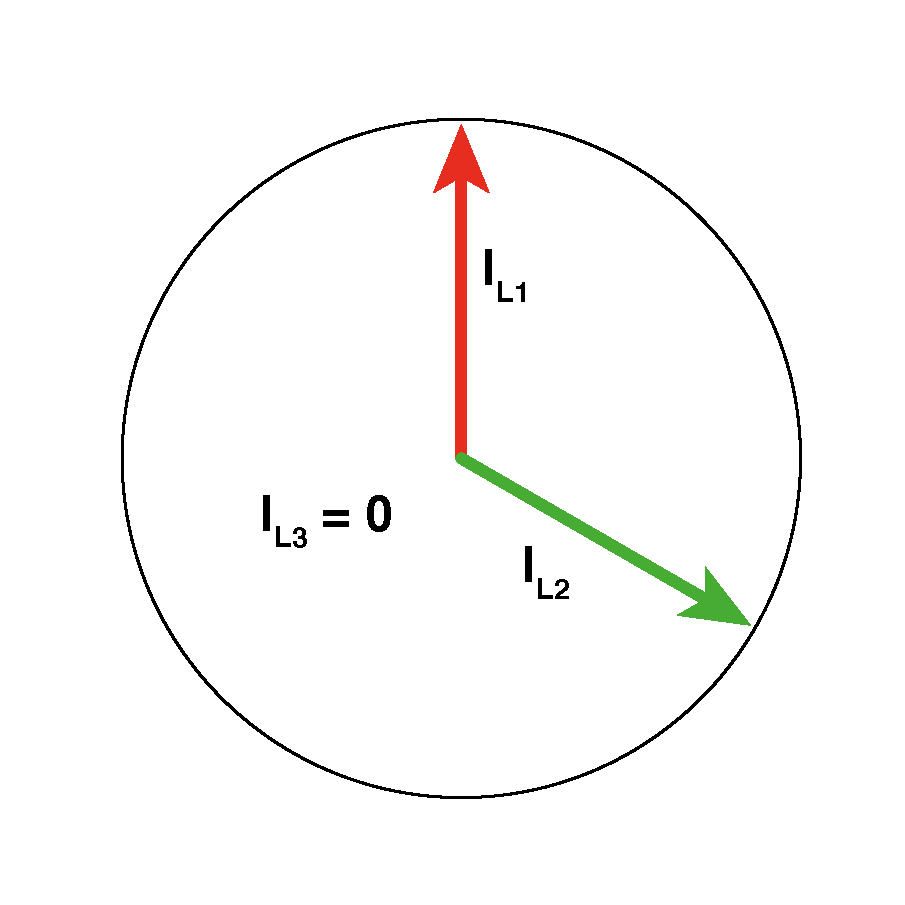
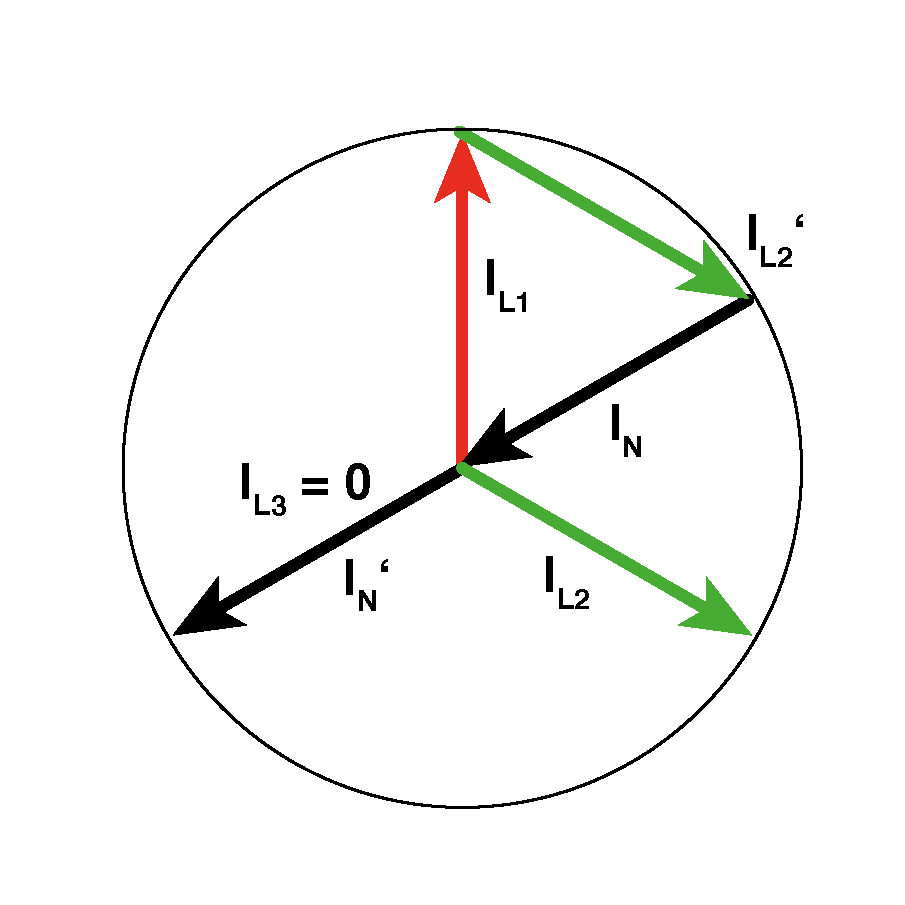
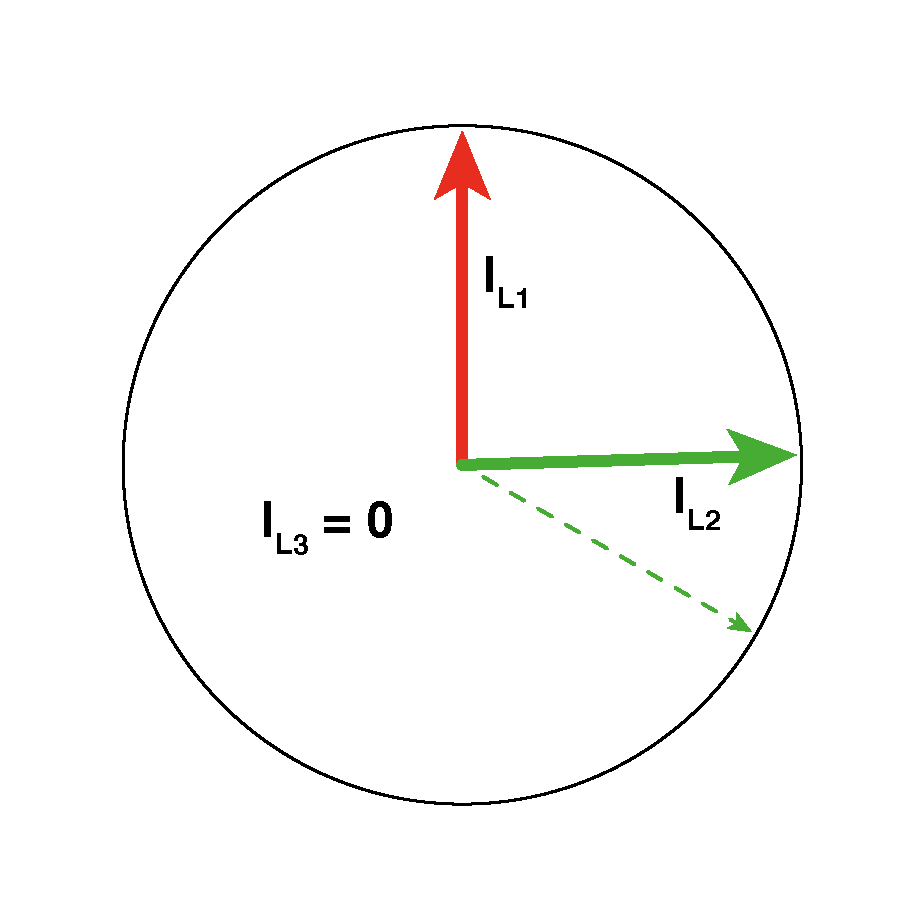
Der Strom IL3 ist "Null". Die Ströme IL1 und IL2 sind gleich groß.
Dieser Fall ist nur ein spezielles Beispiel von (3). Sämtliche Verbraucher an L3 sind abgeschaltet, in diesem Außenleiter fließt kein Strom. Der Strom IN ergibt sich als gleich groß wie IL1 oder IL2. IN fließt in derselben Phasenlage wie der "fehlende" IL3, hier durch IN' verdeutlicht.
IN = IL1 = IL2
Der Phasenwinkel ist gleich dem eines "fiktiven" IL3
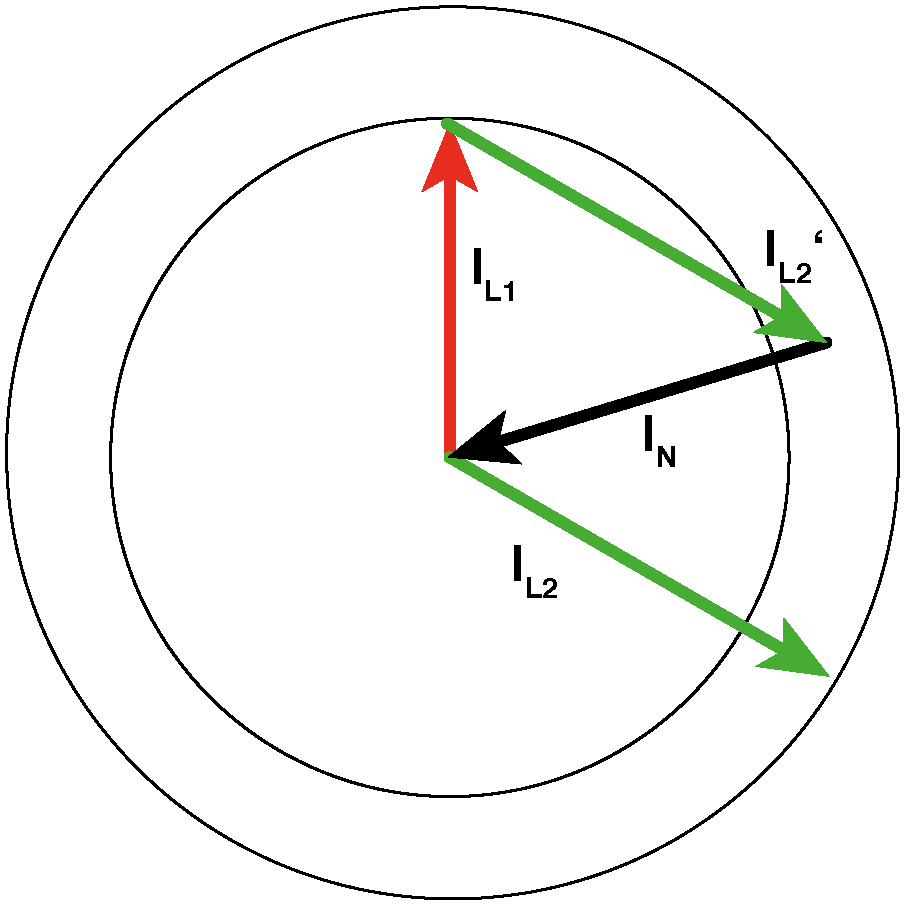
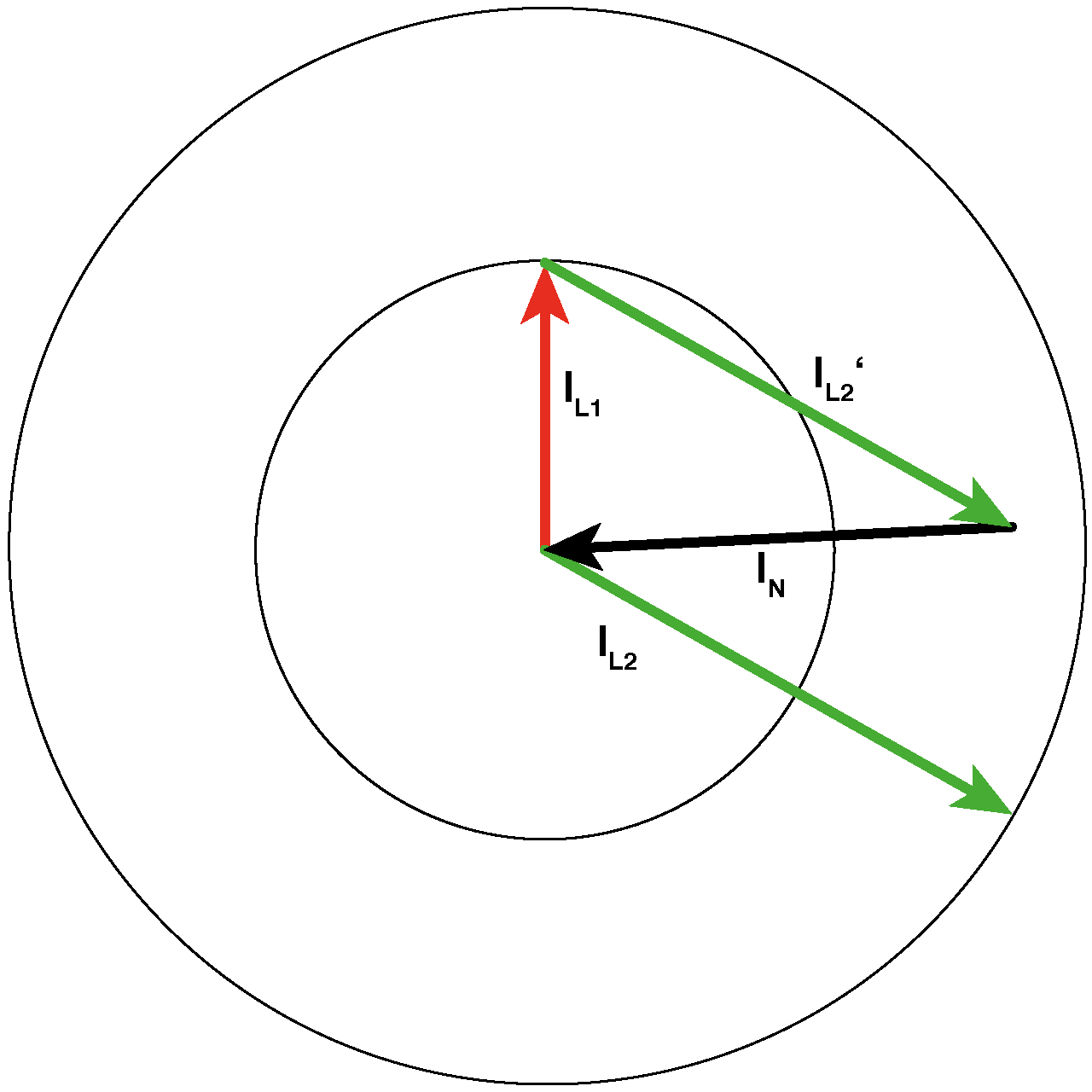
Der Strom IL3 ist "Null". Der Strom IL2 ist (deutlich) größer als der Strom IL1.
Es handelt sich immer noch "nur" um einen speziellen Fall von (3). Hier ist relativ deutlich zu sehen, dass IN nicht größer als IL2 werden kann. Ein Teil von IL2 fließt eben auch über IL1 zurück. Der Phasenwinkel von IN liegt zwischen IL1 und IL2 und nähert sich um so mehr dem Phasenwinkel von IL2 an, je größer dieser Strom wird.
Nun kann man natürlich auch das Extrembeispiel anführen, dass nur genau ein Außenleiter belastet ist und die anderen beiden stromlos sind. Dann ist intuitiv klar, dass der gesamte Strom ILx nur durch den Neutralleiter zurückfließen kann. Damit gilt natürlich IN = ILx. Dieser triviale Fall bringt aber im Folgenden nur wenig Erkenntnisgewinn und ist daher nicht weiter aufgeführt.
IL2 > IN > 0
Phasenlage IN zwischen IL1 und IL2, aber näher am größeren IL2.
In einem rein ohm'sch belasteten Drehstromsystem kann der Strom im Neutralleiter nicht größer werden als der Strom im am stärksten belasteten Außenleiter, weil sich die Ströme der Außenleiter aufgrund der Phasenverschiebung geometrisch ("vektoriell") und nicht arithmetisch addieren. - Diese Aussage gilt unabhängig von einer symmetrischen oder unsymmetrischen Belastung.
Daher muss der Neutralleiter auch keinen größeren Leitungsquerschnitt als die Außenleiter haben. Ein besonderes Überstromschutzorgan ("Sicherung") für den Neutralleiter ist für diesen Fall auch nicht nötig.
Nach dem Zwischenfazit könnte man meinen, dass es keiner weiteren Überlegung zum Neutralleiter bedarf. In der Praxis der realen Drehstromsysteme ist das auch oft so. Im nächsten Kapitel wird aufgezeigt, dass es ganz allgemein betrachtet aber keineswegs der Fall ist.
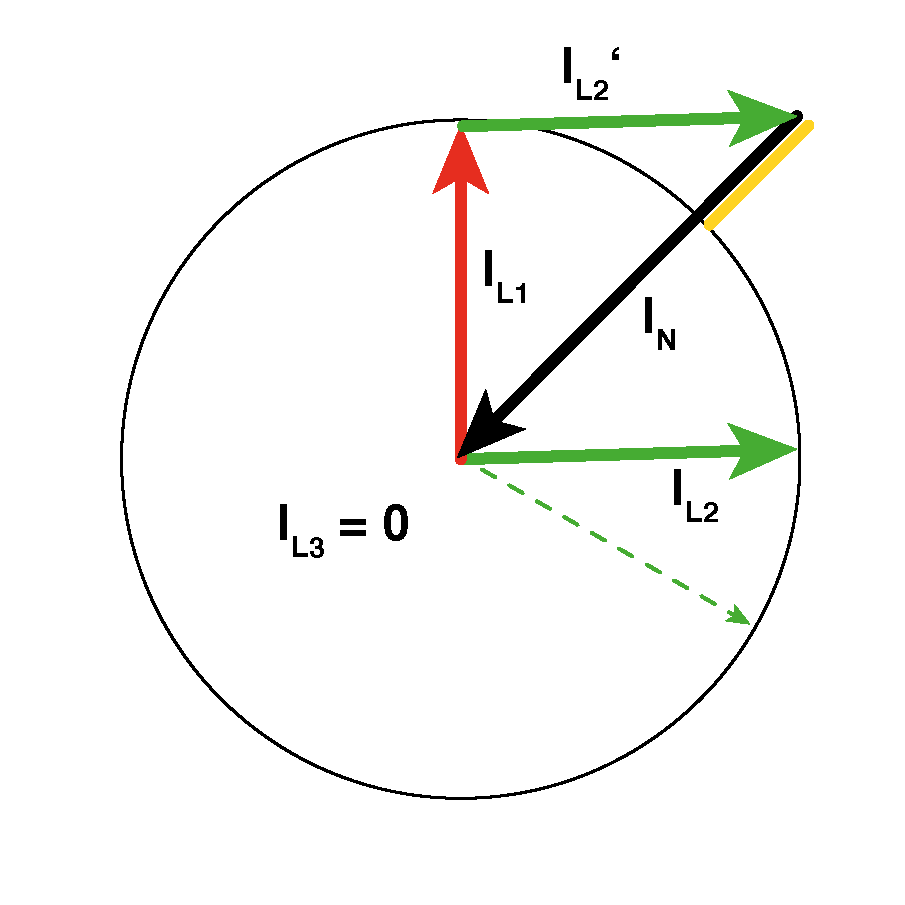
Der Strom IL3 ist weiterhin "Null". Die Ströme IL1 und IL2 sind wieder gleich groß, diesmal aber gegeneinander um weniger als 120° phasenverschoben. An L2 ist ein Verbraucher mit einem cos φ von 0,85 angeschlossen. Es handelt sich also um eine Impedanz bestehend aus einem ohm'schen (Wirk-)Widerstand und einer induktiven (Blind-)Widerstand. Dadurch ist der Strom IL2 gegenüber seiner treibenden Spannung UL2 um 31,79° nacheilend verschoben (cos φ = 0,85 <=> φ = 31,79°). Der gestrichelt eingezeichnete Pfeil zeigt zum Vergleich die Phasenlage eines rein ohm'schen Verbrauchers.
Dadurch beträgt die Phasenverschiebung von IL1 und IL2 nun nicht mehr 120°, sondern nur noch 88,21°. Das hat für die geometrische Addition der beiden Ströme erhebliche Konsequenzen. Die Pfeilspitze von IL2' zeigt deutlich aus dem Kreis der beiden Zeiger heraus. Dadurch ist IN größer als IL2 und IL1 (orange markiert)!
Es braucht also nicht viel, um den IN größer als den größten Außenleiterstrom werden zu lassen. Ein Verbraucher mit einem cos φ von 0,85 kann dafür unter Umständen genügen, und ein cos φ von 0,85 ist nicht einmal ein "besonders schlechter" Wert (aber natürlich auch kein "guter").
Für das Beispiel gilt also:
IN > IL2 mit IL1 = IL2
Und ja, bereits ein kleiner (auch rein ohm'scher) IL3 würde genügen, um den IN erst wieder "im Kreis" beginnen zu lassen und damit kleiner als den größten Außenleiterstrom zu machen. - Aber darauf verlassen, dass es diesen gibt, kann man sich eben nicht.
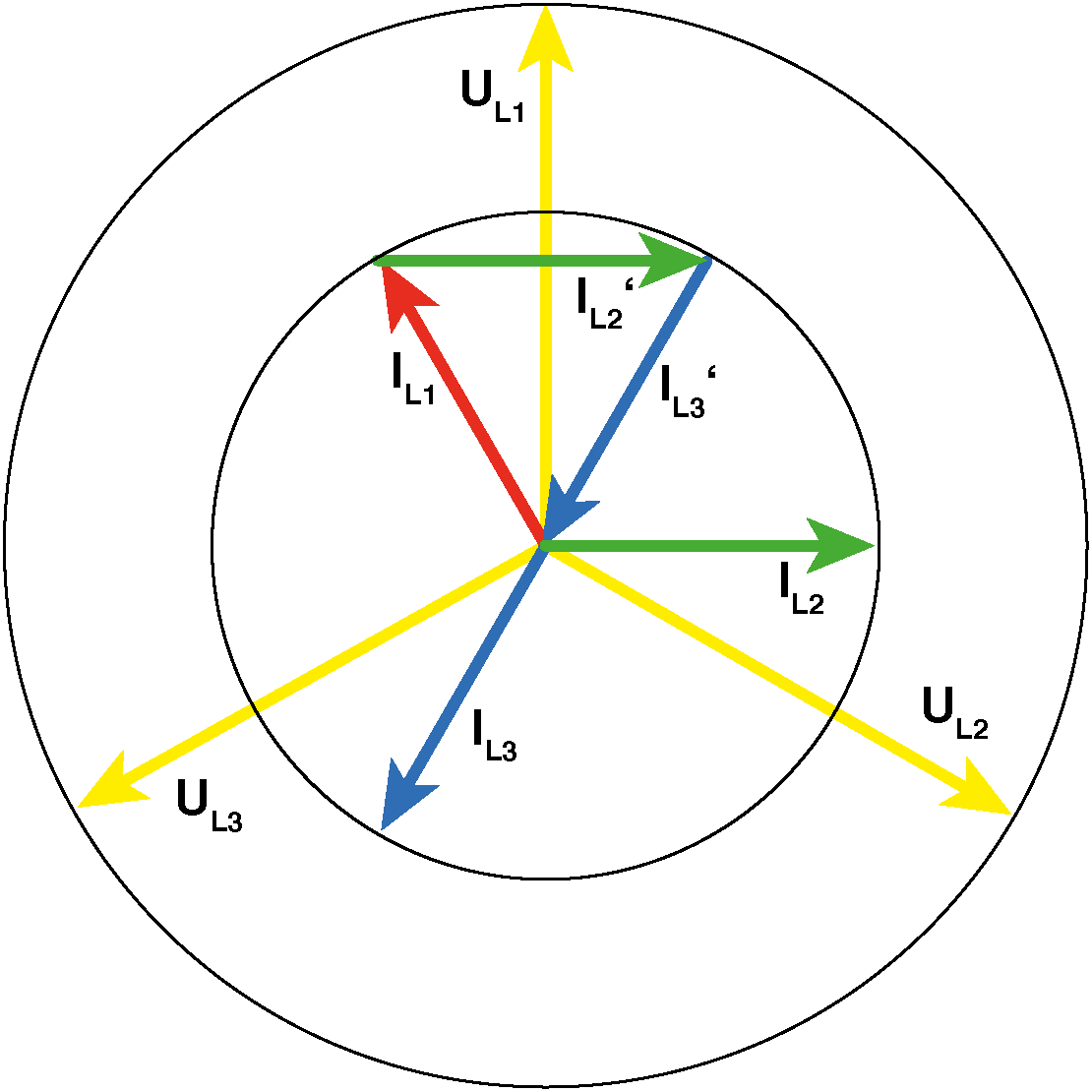
Die Hoffnung besteht darin, dass "sich schon irgendwie alles herausmittelt", weil die Phasen in Summe einigermaßen gleichmäßig belastet sind, und das nicht nur was den Betrag der Ströme angeht, sondern auch deren Phasenlage!
Wenn sich nämlich das gesamte System der Ströme verdreht, fließen zwar erhebliche so genannte "Blindströme", welche die Stromstärken im Betrag unnötig groß machen, aber für den Neutralleiter heißt das trotzdem, dass der in ihm fließende Strom relativ klein oder sogar "Null" ist.
Das gezeigte Beispiel könnte ein Drehstrommotor mit einem cos φ von 0,87 sein (Phasenwinkel rund 30°). Er belastet das Netz hinsichtlich Strom und Phasenlage "symmetrisch".
Wenn auch gegenüber der Spannung verdreht, gilt dasselbe wie in (1):
IN = 0
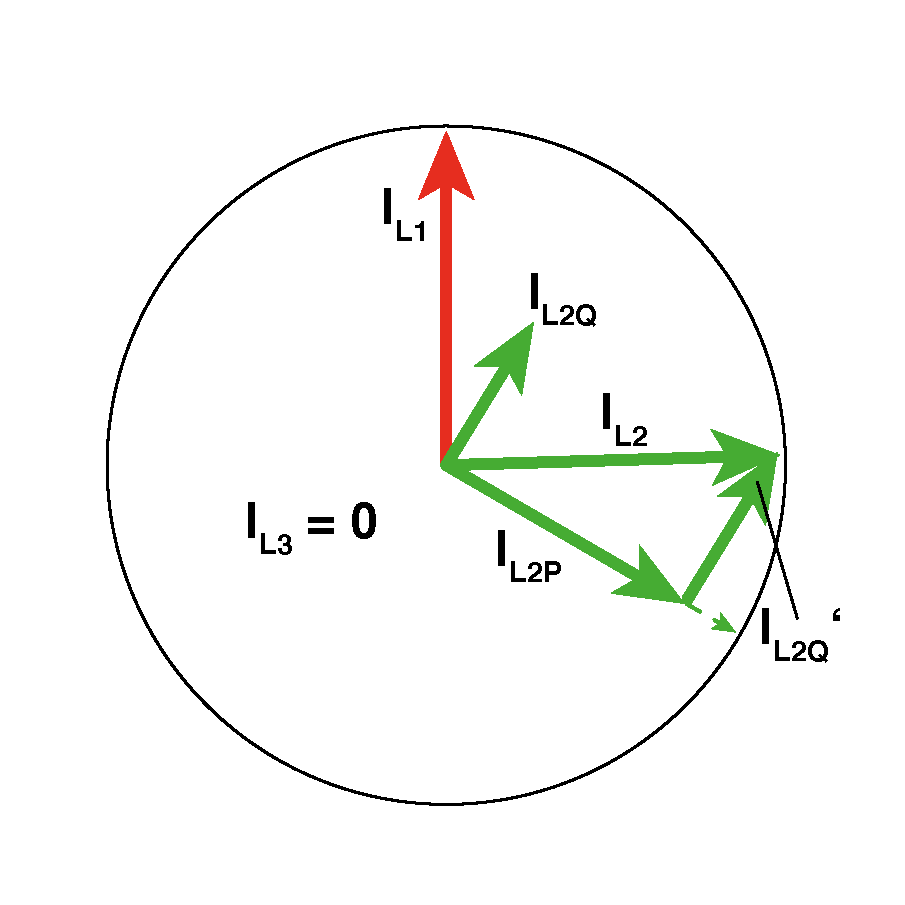
Um zu verstehen, was Kompensation ist, muss man zunächst verstehen, wie die Phasenverschiebung von IL2 überhaupt zustande kommt. Der Strom IL2 besteht aus zwei Anteilen, die genau 90° gegeneinander phasenverschoben sind. Der eine Anteil ist der Strom IL2P durch den Ohm'schen Widerstand, dieser liegt mit der Spannung in Phase und erzeugt die Wirkleistung P, der andere Anteil IL2Q entsteht durch den induktiven (durch Spulen verursachten) Anteil, der aufgrund seiner 90° Phasenverschiebung zur Spannung nur Blindleistung Q erzeugt.
Werden nun IL2P und IL2Q (anschaulich verschoben als IL2Q') grafisch addiert, ergibt sich der Gesamtstrom IL2.
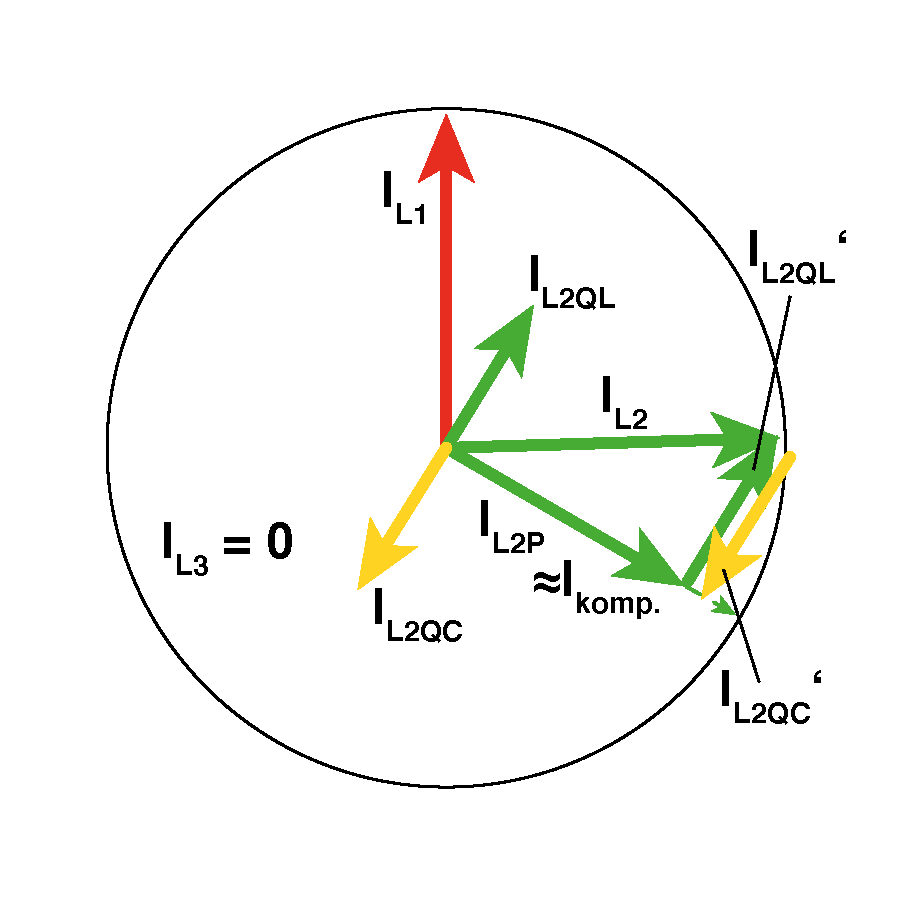
Blindströme (und Blindleistungen) gibt es in zwei möglichen Ausprägungen: Induktive Blindströme (und -leistungen) entstehen durch Spulen (Induktivitäten, L) und werden hier IL2QL genannt. Sie eilen der Spannung 90° nach. Kapazitive Blindströme (und -leistungen) entstehen durch Kondensatoren (Kapazitäten, C) und werden hier IL2QC genannt. Sie eilen der Spannung um 90° voraus. Das heißt IL2QL und IL2QC sind gegeneinander um 180° phasenverschoben, sie zeigen genau in entgegengesetzte Richtungen.
Kompensation bedeutet nun, dass man dem (im Allgemeinen anwendungsbedingten) Blindstrom IL2QL, der zur Verschiebung der Phase des Gesamtstroms IL2 führt, einen künstlich erzeugten, nahezu gleich großen Strom IL2QC entgegensetzt.
Das hat zwei unmittelbare Vorteile: Die grafische Addition (Hinweis: IL2QC' ist nur zur Übersichtlichkeit neben IL2QL' eingezeichnet, sie müssten direkt übereinander liegen) aller drei Ströme führt dazu, dass IL2 wieder (nahezu) in Phase mit seiner Spannung UL2 liegt und auch noch (unter Umständen deutlich) kleiner wird. Dadurch wird auch der effektiv auf den Leitungen transportierte Strom kleiner, weil die Energie nur zwischen den installierten Spulen und Kondensatoren "hin- und hergeschoben" wird. Das ist zwar auch nicht verlustfrei, aber viel besser als die Energie über den gesamten Weg zwischen Quelle und Verbraucher hin- und herzutransportieren.
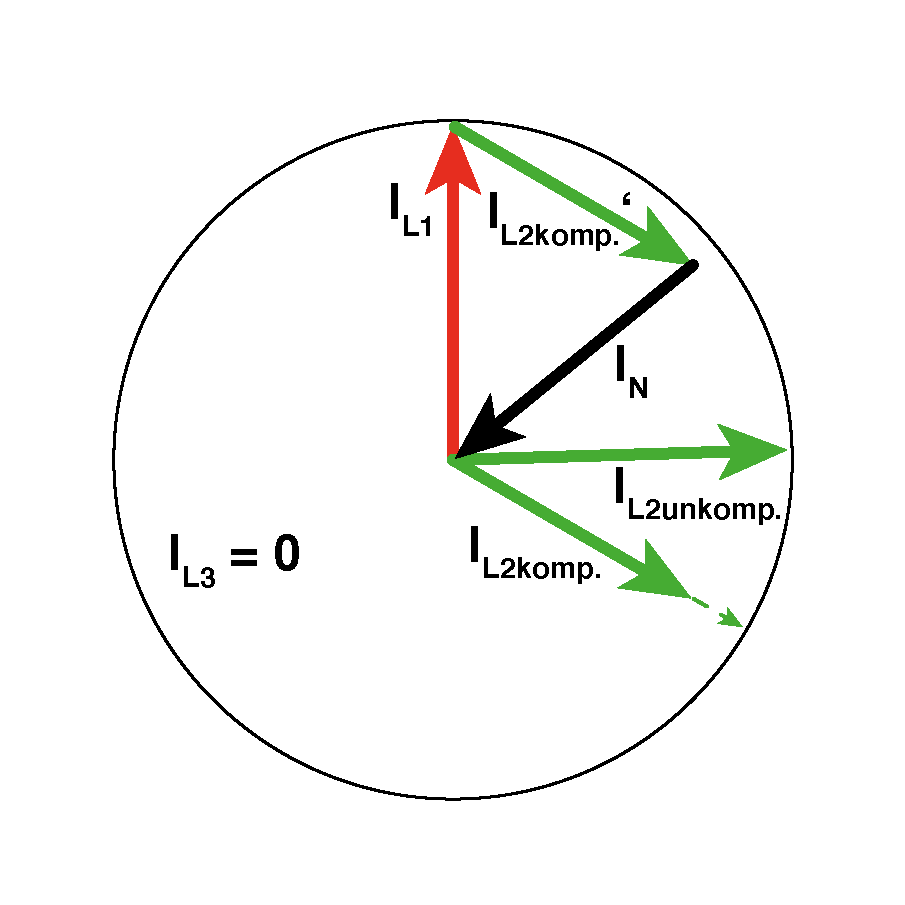
Der dritte und in dieser Betrachtung entscheidende Vorteil ist, dass mit Kompensation (natürlich für alle potenziell phasenverschobenen Ströme!) wieder eine Phasenverschiebung von (nahezu) 120° zwischen IL1 und IL2 und IL2 sichergestellt ist. Und damit gilt für den Neutralleiter wieder der gewünschte, weil "sichere" Fall:
IN ist kleiner als der größte Außenleiterstrom.
In einem rein ohm'sch belasteten Drehstromsystem kann der Strom im Neutralleiter nicht größer werden als der Strom im am stärksten belasteten Außenleiter, weil sich die Ströme der Außenleiter aufgrund der Phasenverschiebung geometrisch ("vektoriell") und nicht arithmetisch addieren. - Diese Aussage gilt unabhängig von einer symmetrischen oder unsymmetrischen Belastung.
Sind aber die Phasen des Drehstromsystem nicht jeweils 120° gegeneinander phasenverschoben kann der Strom im Neutralleiter sehr wohl größer werden als der Strom im am stärksten belasteten Außenleiter!
Ein unregelmäßig in den Phasen verschobenes Drehstromsystem kann (und sollte unbedingt!) durch Kompensation der Phasenverschiebung aller(!) Phasen zu einem (annähernd) rein ohm'sch belasteten Drehstromsystem gemacht werden. Dann gelten wieder die dort beschriebenen Verhältnisse und der Neutralleiter ist nicht durch Überlastung gefährdet.
Aber:
Heutzutage tritt durch den nicht-sinusförmigen Verlauf von Strömen in Schaltnetzteilen und Frequenzumrichtern zusätzlich und vermehrt das Problem von Oberwellen im Drehstromsystem auf. Diese addieren sich sozusagen "in mathematisch unglücklicher Weise" im Neutralleiter und können ihn dadurch völlig unabhängig von Phasenverschiebung und unterlassener Kompensation überlasten. - Dieses sehr wohl ernst zu nehmende Phänomen wurde hier aber bewusst nicht behandelt.
Eine gut verständliche Erklärung zum Thema Oberwellen präsentiert Andreas Blomberg in einem seiner Youtube-Videos:
Oberwellen im Drehstromsystem (Teil 9) Neutralleiterstrom / Oberschwingungen / Elektrotechnik
Noch ein letzter Hinweis zur Kompensation:
Im Allgemeinen werden Blindleistungen kompensiert und nicht wie hier im Beispiel angeführt Blindströme. Das kommt für das Beispiel aber auf dasselbe raus. Außerdem gibt es (die im Zweifelsfall klar zu bevorzugenden) lokalen Kompensationen unmittelbar an jedem Verbraucher und die (zumindest nachträglich leichter zu installierenden, aber weniger guten) Zentralkompensationen. Letztere stellen nur vernünftige Zustände auf der Versorgerseite sicher, in der eigenen Installation können dann immer noch stark ungleichmäßig phasenverschobene Ströme auftreten. Lokale Kompensationen stellen für jeden einzelnen Verbraucher günstige Verhältnisse her.
Aber das ist ein anderes Thema, das im Detail auch wesentlich ausführlicher behandelt werden muss.
|
Was macht |